Markets-Web.ru

Следует определить, какие из исходных сплавов и в каких количествах нужно использовать для получения требуемого сплава, чтобы суммарные затраты на исходные сплавы были минимальными.

Сформулируем экономико-математическую модель данной задачи. Обозначим через х1 х2, x3 х4 х5

искомые количества исходных сплавов. Тогда целевая функция примет вид:

При этом существуют следующие условия:

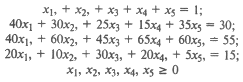
Сформулированная задача, как и предыдущая, решается методами линейного программирования.

Модели оптимального раскроя промышленных материалов.

Сущность оптимального раскроя состоит в разработке таких технологически допустимых раскройных планов, при которых из стандартных единиц раскраиваемых ресурсов получается необходимый комплект заготовок требуемого размера, а критерий оптимальности заключается в сведении к минимуму либо общей величины отходов кроя, либо количества раскраиваемых единиц ресурсов.

Формулировка задачи оптимального раскроя зависит от формы раскраиваемого материала, который может быть длинномерным, листовым, рулонным и т.д. Сформулируем экономико-математическую модель задачи оптимального раскроя по одному измерению длинномерных материалов (прутков, труб, профильного проката и др.). Примем следующие обозначения:

L – длина исходного материала;

i – номер (индекс) вида требуемых заготовок, i = 1, 2 . т;

li – длина заготовки i-го вида;

Аi – требуемое число заготовок i-го вида (не менее);

j - номер варианта раскроя, j = 1, 2 . n;

aj – количество заготовок i-го вида при раскрое единицы исходного материала по j-му варианту;

сij – длина отхода по j-му варианту.

Пусть х1 - количество единиц исходного материала, раскраиваемых по i-му варианту. Целевая функция по критерию минимума отходов имеет вид:

По критерию минимума раскраиваемых единиц исходного материала уравнение может быть таким:

Это верно при соблюдении следующих условий:

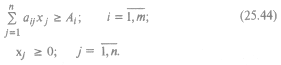
Получилась задача линейного программирования, которую надо пополнить требованием целочисленности величины хj.

Заметим, что во многих случаях решения задач с обеими указанными целевыми функциями совпадают.

Наиболее трудоемкий этап в процессе построения модели рассматриваемой задачи заключается в определении всех возможных вариантов раскроя. Исходные соотношения для составления вариантов раскроя следующие:

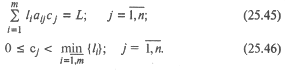
Условие (25.46) означает, что длина отхода для любого варианта раскроя должна быть меньше, длины самой короткой заготовки (это является признаком полноценности варианта).

Рассмотрим пример. Снабженческо-сбытовая фирма получает от поставщиков прутки стального проката длиной 600 см. Согласно заявкам потребителей требуются заготовки трех видов в следующих количествах: 150 тыс. шт. длиной 250 см, 140 тыс. шт. длиной 190 см и 48 тыс. шт. длиной 100 см. Сформулируем экономико-математическую модель задачи оптимального раскроя с минимумом отходов. Составим таблицу возможных вариантов раскроя, при этом в первом блоке имеют место варианты раскроя, дающие все три вида заготовок, во втором - дающие заготовки второго и третьего вида, а в третьем – дающие заготовки только третьего вида.

Таблица 25.5

Возможные варианты раскроя