Markets-Web.ru

Оптимизационными

задачами,

в экономике называются экономико-математические задачи, цель которых состоит в нахождении наилучшего (оптимального) с точки зрения некоторого критерия (критериев) варианта использования наличных ресурсов (материальных, временных и т.д.). Решаются такие задачи с помощью оптимизационных моделей методами математического программирования.

В отличие от дескриптивных, т.е. описательных моделей, примером которых могут служить рассмотренные выше балансовые модели, оптимизационные модели наряду с уравнениями или неравенствами, описывающими взаимосвязи между переменными, содержат также критерий для выбора, называемый функционалом, или целевой функцией. Таким образом, общая структура этих моделей состоит из целевой функции, принимающей значения в пределах ограниченной условиями задачи области (области допустимых решений), и из ограничений, характеризующих эти условия. Целевая функция в самом общем виде определяется тремя моментами: управляемыми переменными, неуправляемыми параметрами (зависящими, например, от внешней среды) и видом (формой) зависимости между ними (видом функции). Если обозначить критерий оптимальности через U, управляемые переменные – = (xi), параметры – = (pj), заданные пределы (область) изменения управляемых переменных – М, то общий вид оптимизационной модели будет следующим:

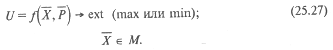
Задачи вида (25.27) решаются методами математического программирования, которое включает в себя линейное, нелинейное, динамическое, целочисленное программирование и т.д. Выбор методов математического программирования для решения оптимизационных задач определяется видом целевой функции f, видом ограничений, определяющих область М, и специальными ограничениями на управляемые переменные (например, требованием их целочисленности). Решение задачи получения управнения (25.27) обычно называется оптимальным решением, или оптимальным планом.

Рассмотрим прежде всего оптимизационные задачи, сводящиеся к задачам линейного программирования (ЗЛП). В общем виде такая задача может быть сформулирована, например, следующим образом.

Найти вектор = (х1, х2 . хn), максимизирующий линейную целевую функцию: , а также удовлетворяющий линейным функциональным ограничениям:

Кроме того, искомый вектор должен удовлетворять и прямым ограничениям:

Задача (25.28) может быть записана в канонической форме, при которой функциональные ограничения имеют вид равенств. Это достигается путем прибавления к левым частям этих ограничений т дополнительных неотрицательных переменных. ЗЛП в канонической форме решается симплексным методом, в то же время для некоторых ЗЛП специального вида разработаны соответствующие методы (алгоритмы) решения.

Некоторые из них не связаны непосредственно с алгоритмом симплексного метода, как, например, метод потенциалов для решения транспортной задачи; другие же в качестве составных элементов используют вычислительные процедуры симплексного метода. В качестве примера последних можно привести метод Гомори (метод отсечений) для решения задач линейного целочисленного программирования.

Оптимизационные задачи, сводящиеся к задачам линейного программирования, широко используются в процессе экономико-математического моделирования (они рассматриваются ниже). Однако задачами линейного программирования не исчерпываются все виды оптимизационных экономических задач, так как во многих случаях целевая функция задачи и ограничения на область допустимых решений не удовлетворяют условиям линейности. Тогда применяются специальные методы нелинейного программирования, например метод множителей Лагранжа, динамического и имитационного программирования и др.