Markets-Web.ru

Ограничения формулируются следующим образом:

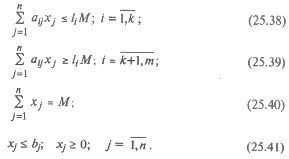
Ограничения (25.38) относятся к элементам, ухудшающим качество, (25.39) – к элементам, улучшающим качество, (25.40) - к плану производства, (25.41) – к ограничению ресурсов.

Задача о смесях решается с применением методов линейного программирования.

Рассмотрим следующий пример. В изготовленном на предприятии бензине А 76 октановое число должно быть не ниже 76, а содержание серы – не более 0,3%. Данные об используемых компонентах приведены в табл. 25.3.

Таблица 25.3

Используемые в автомобильном бензине компоненты

Требуется определить, сколько тонн каждого компонента нужно взять для получения 1000 т бензина А 76, чтобы при этом себестоимость бензина была минимальной.

Пусть х1х2х3х4 – оптимальные количества соответствующих компонентов.

Целевая функция задачи:

f() = 40x1 + 45х2 + 60х3 + 90x4 → min;

Ограничение по октановому числу: 68x1 + 72x2 + 80х3 + 90x4 ≥ 76 · 1000.

Ограничение по содержанию серы: 0,35x1, + 0,35x2 + 0,3x3 + 0,2х4 < 0,3 · 1000.

Ограничение по объему готовой продукции: х1 + x2 + х3 + x4 = 1000.

Ограничения по имеющимся ресурсам: x1 ≤ 700; х2 ≤ 600; х3 ≤ 500; х4 ≤ 300.

Условие неотрицательности переменных: x1, x2, х3, х4 ≥ 0.

Сформулированная экономико-математическая модель сводится к задаче линейного программирования. Ее решение симплексным методом на ЭВМ дает оптимальный план составления смеси: Х = (571; 0; 143; 286; 0; 0; 129; 600; 357; 14). Следовательно, в рассматриваемом случае следует использовать такую смесь: 571 т компонента 1; 143 т компонента 3; 286 т компонента 4. При этом себестоимость 1000 т бензина А 76 будет составлять 57 160 денежных единиц.

Рассмотрим еще один пример: получение требуемого сплава. Пусть требуется изготовить некоторую единицу объема сплава, содержащего 15% олова, 55% цинка и 30% свинца. Данные об имеющихся исходных сплавах заданы в табл. 25.4.

Таблица 25.4

Характеристики исходных сплавов