Markets-Web.ru

Рассмотрим сначала однофакторную линейную модель зависимости расходов на питание (у) от величины душевого дохода семей (х1). Она выражается линейной функцией следующего вида:

Параметры a0 и а1 можно найти, решив систему нормальных уравнений, которая, в свою очередь, формируется с применением метода наименьших квадратов. Система нормальных уравнений для рассматриваемого случая имеет вид:

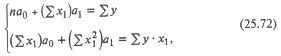
где суммирование проводится по всем n группам. Используя данные табл. 25.7, получим систему уравнений:

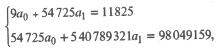
решением которой являются значения a0 = 549,68 и а1 = 0,1257.

Таким образом, модель имеет вид;

Уравнение (25.73) называется уравнением регрессии, коэффициент а1 называется коэффициентом регрессии. Направление связи между у и х1 определяет знак коэффициента регрессии а1 (в нашем случае данная связь является прямой). Теснота этой связи определяется коэффициентом корреляции:

где Sy есть средняя квадратическая ошибка выборки у в табл. 25.7. Она находится по формуле:

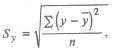
где – средняя арифметическая значений у, а – средняя квадратическая ошибка нашего уравнения (25.73). Последняя определяется следующим образом:

где есть соответствующее значение, вычисленное по модели (25.73). В этих формулах, как и ранее, суммирование ведется по всем группам.

Чем ближе значение коэффициента корреляции к единице, тем теснее корреляционная связь. В нашем примере Sy2 = 454 070, = 63 846, следовательно:

Полученное значение свидетельствует, что связь между расходами на питание и душевым доходом очень тесная. Величина называется коэффициентам детерминации и показывают долю изменения (вариации) результативного признака под действием факторного признака. В нашем случае = 0,859; это означает, что фактором душевого дохода можно объяснить почти 86% изменения расходов на питание.

Рассмотрим теперь двухфакторную линейную модель зависимости расходов на питание (у) от величины душевого дохода семей (х1) и размера семей (х2). Множественный (многофакторный) корреляционно-регрессивный анализ решает три задачи: определяет форму связи результативного признака с факторными, выявляет тесноту этой связи и устанавливает влияние отдельных факторов. В нашем случае эта модель имеет вид:

Параметры модели a0, а1 и а2 находятся путем решения системы нормальных уравнений:

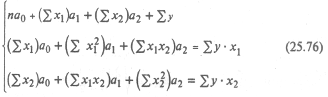
Используя данные табл. 25.7, получим систему нормальных уравнений в таком виде:

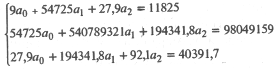
Решая эту систему (например, методом Гаусса), получим: a0 = 18,63; а1 = 0,0985; a2 = 224,6, так что модель (25.75) имеет вид:

Для определения тесноты связи предварительно вычисляются парные коэффициенты корреляции . Например:

где черта над символами означает среднюю арифметическую, a Sy и Sx1 – средние квадратические ошибки соответствующих выборок из табл. 27.7. Их можно вычислить следующим образом: