Markets-Web.ru

Таким образом, имеет место определение

: коэффициент прямых материальных затрат аij показывает, какое количество продукции i-й отрасли необходимо для производства единицы продукции j-й отрасли (с учетом только прямых затрат).

Используя формулу (25.4), систему уравнений баланса (25.2) можно переписать в следующем виде:

Если ввести в рассмотрение матрицу коэффициентов прямых материальных затрат А = (aij), а также вектор-столбец валовой продукции X и вектор-столбец конечной продукции Y:

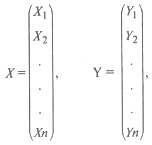
то система уравнений (25.5) в матричной форме примет такой вид:

X = AX + Y. (25.6)

Система уравнений (25.5), или она же в матричной форме (25.6), называется экономико-математической моделью межотраслевого баланса (моделью В. Леонтьева, моделью «затраты -выпуск»). С ее помощью можно выполнять три варианта расчетов.

1. Задав в модели величины валовой продукции каждой отрасли (Xi), можно определить объем конечной продукции каждой отрасли (Yi):

Y = (E - A) · X. (25.7)

2. Задав величины конечной продукции всех отраслей (Yi), можно определить величины валовой продукции каждой отрасли (Xi):

X = (E – A)-1 · Y. (25.8)

3. Задав для ряда отраслей величины валовой продукции, а для всех остальных отраслей объемы конечной продукции, можно найти величины конечной продукции первых отраслей и объемы валовой продукции вторых. В этом варианте расчета удобнее пользоваться не матричной формой модели (25.6), а системой линейных уравнений (25.5).

В формулах (25.7) и (25.8) Е обозначает единичную матрицу n-го порядка, а (Е – A)-1 обозначает матрицу, обратную матрице (Е – А). Если определитель матрицы (Е – А) не равен нулю, т.е. эта матрица невырожденная, то обратная ей матрица существует. Обозначим последнюю так:

В = (Е - А)-1

Тогда систему уравнений в матричной форме (25.8) можно записать в виде:

X = BY. (25.8)

Элементы матрицы В будем обозначать через bij, тогда из матричного уравнения (25.8') для любой i-й отрасли можно получить следующее соотношение:

Из соотношений (25.9) следует, что валовая продукция выступает как взвешенная сумма величин конечной продукции, причем весами являются коэффициенты bij, которые показывают, сколько всего нужно произвести продукции i-й отрасли для выпуска в сферу конечного использования единицы продукции j-й отрасли. В отличие от коэффициентов прямых затрат аij коэффициенты bij называются коэффициентами полных материальных затрат и включают в себя как прямые, так и косвенные затраты всех порядков. Если прямые затраты отражают количество средств производства, израсходованных непосредственно при изготовлении данного продукта, то косвенные относятся к предшествующим стадиям производства и входят в производство продукта не прямо, а через другие (промежуточные) средства производства. Более детально этот вопрос рассматривается в следующем разделе.

Дадим определение

коэффициента полных затрат: коэффициент полных материальных затрат bij показывает, какое количество продукции i-й отрасли нужно произвести, чтобы с учетом прямых и косвенных затрат этой продукции получить единицу конечной продукции j-й отрасли.

Коэффициентами полных материальных затрат можно пользоваться, когда необходимо определить, как скажется на валовом выпуске некоторой отрасли предполагаемое изменение объемов конечной продукции всех отраслей:

где ∆Хij, и ∆Yj – изменения (приросты) величин валовой и конечной продукции соответственно.

Коэффициенты прямых и полных материальных затрат, связь между ними, методы расчета.

Переходя к анализу модели МОБ, необходимо прежде всего рассмотреть основные свойства матрицы коэффициентов прямых материальных затрат А. Коэффициенты прямых затрат по определению являются неотрицательными, следовательно, матрица А в целом может быть названа неотрицательной: А ≥ 0. Так как процесс воспроизводства нельзя осуществлять, если для собственного воспроизводства в отрасли затрачивается большее количество продукта, чем создается, то очевидно, что диагональные элементы матрицы А меньше единицы: аii < 1.

Система уравнений МОБ является отражением реальных экономических процессов, в которых содержательный смысл могут иметь лишь неотрицательные значения валовых выпусков, поэтому вектор валовой продукции состоит из неотрицательных компонентов. Экономическая система обеспечивает положительный конечный выпуск по всем отраслям, если матрица коэффициентов прямых материальных затрат удовлетворяет условию продуктивности: X > АХ. Это означает существование положительного вектора конечной продукции Y > 0 для модели МОБ (25.6).